NOÇÕES DE LÓGICA MATEMÁTICA
O CÁLCULO PROPOSICIONAL E A ÁLGEBRA DOS CONJUNTOS

O Cálculo Proposicional e a Álgebra dos Conjuntos possuem estruturas semelhantes.
Toda fórmula do Cálculo Proposicional determina uma operação correspondente entre conjuntos :

As variáveis proposicionais podem servir como variáveis simbolizando conjuntos na nova expressão.

Exemplo: (( p Ú q) Ù ~ p)corresponde a (( p È q ) Ç p’)

Podemos expressar, as operações entre conjuntos através dos DIAGRAMAS DE EULER-VENN (John Venn 1834-1923) que são úteis na verificação de propriedades de operações entre conjuntos, mas não devem ser considerados instrumentos de prova matemática rigorosa. Verifique seu conhecimento com estas operações considerando 2 conjuntos ou  3 conjuntos.

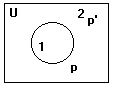
1.COMPLEMENTAÇÃO : p’que corresponde à NEGAÇÃO :~p
p ~ p
1 V  F
2 F V

onde as linhas (1) e (2) da tabela correspondem às regiões (1) e (2) do diagrama respectivamente.

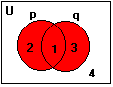
2.UNIÃO : p È q que corresponde à DISJUNÇÃO: p Úq
          p È q

p
q
p Ú q
1 V V
V
2 V F
V
3 F V
V
4 F F
F

as linhas (1), (2), (3) e (4) da tabela correspondem às regiões (1), (2), (3) e (4) do diagrama respectivamente.
A região hachurada no diagrama corresponde às linhas da tabela onde a fórmula p Ú q assume valor V.

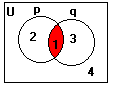
3. INTERSECÇÃO : p Ç q que corresponde à CONJUNÇÃO: p Ù q
            p Ç q
p q p Ùq
1 V V
V
2 V F
F
3 F V
F
4 F F
F
A região hachurada do diagrama corresponde à linha (1) da tabela, onde a fórmula pÙq assume valor V.

A figura abaixo forma um Diagrama de Venn apropriado para três conjuntos. Temos 8 regiões que correspondem, respectivamente, às 8 linhas da tabela-verdade ao lado do diagrama :
 
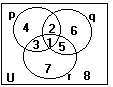p q
r
1 V V
V
2 V V
F
3 V F
V
4 V F
F
5 F V
V
6 F V
F
7 F F
V
8 F F
F

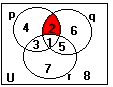
Exemplo: O diagrama de Venn abaixo corresponde à fórmula ~((p Ù q) ® r) e à expressão (p Ç q) Ç r’. O valor V da fórmula (última coluna) corresponde à região 2 do diagrama de Venn.
p
q
r
 ~((p Ù q) ® r )
V
V
V
 F         V      V   V
V
V
F
 V        V      F    F
V
F
V
 F         F      V    V
V
F
F
 F         F      V    F 
F
V
V
 F         F      V    V
F
V
F
 F         F      V    F
F
F
V
 F         F      V    V
F
F
F
 F         F      V    F

CELINA ABAR
- 2004 -